第三节 - 算法的描述与分析
发布时间:2020-09-20 10:24来源:未知
第三节 算法的描述与分析
一、算法的描述
算法:是对问题求解步骤的一种描述。算法是由若干条指令组成的有穷序列,其中每条指令表示一个或多个操作。算法还必须满足以下五个准则:
(1)输入。算法开始前必须给算法中用到的变量初始化,一个算法的输入可以包含零个或多个数据。
(2)输出。算法至少有一个或多个输出。
(3)有穷性。算法中每一条指令的执行次数都是有限的,而且每一步都在有穷时间内完成,即算法必须在执行有限步后结束。
(4)确定性。算法中每一条指令的含义都必须明确,无二义性。
(5)可行性。算法是可行的,即算法中描述的操作都可以通过有限次的基本运算来实现。
本教材都采用类C语言描述算法。
真题选解
(例题·单选题)算法指的是( )
A.计算机程序
B.解决问题的计算方法
C.排序算法
D.解决问题的有限运算序列
二、算法分析
例:百钱百鸡问题。100个钱买100只鸡,其中公鸡5钱1只,母鸡3钱1只,小鸡1钱3只,求公鸡、母鸡、小鸡各买多少只?
分析:设公鸡、母鸡、小鸡分别买a、b、c只,则
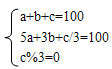
//函数返回值为满足问题的解数, g[], m[], s[]分别存放不同解的公鸡、母鸡和小鸡数
int chicken question(int g[],int m[],int s[])
{ int a,b,c,k=0;
for(a=0;a<=100;a++)
for(b=0;b<=100;b++)
for(c=0;c<=100;c++)
if((a+b+c==100)&&(5*a+3*b+c/3==100)&& (c%3==0))
{ g[k]=a;m[k]=b;s[k]=c;
k=k+1;
}
return k;
}
算法需要执行101×101×101约100万次
对上述算法是完全可以改进的。
int chicken question(int g[],int m[],int s[])
{ int a,b,c,k=0;
for(a=0;a<=20;a++)
for(b=0;b<=33;b++)
{ c=100-a-b;
if((5*a+3*b+c/3==100)&&(c%3==0))
{ g[k]=a;m[k]=b;s[k]=c;
k=k+1;
}
}
return k;
}
算法需要执行21×34=714次。因此,设计一个好的算法,对提高程序的执行效率是至关重要的。
1、评价算法的指标:
(1)算法的正确性,是指对于一切合法的输入数据,该算法经过有限时间的执行都能得到正确的结果。
(2)执行算法所耗费的时间,即时间复杂性。
(3)执行算法所耗费的存储空间,主要是辅助空间,即空间复杂性。
(4)算法应易于理解、易于编程,易于调试等,即可读性和可操作性。
2、算法的时间复杂度
时间复杂度:是某个算法的时间耗费,它是该算法所求解问题规模n的函数。记作T(n)=O(f(n))。
例:求下面程序段的算法时间复杂度。
x=0;
for(i=2;i<=n;i++)
for(j=2;j<=i-l;j++)
x=x+1;
算法时间复杂度只需要求出它关于n的增长率或阶即可。上述语句x=x+l执行次数关于n的增长率为n2,所以该程序段的算法时间复杂度为O(n2)。
如果一个算法的执行时间是一个与"问题规模"无关的常数,即使是一个较大的常数,该算法的时间复杂度都为常数阶,记作T(n)=O(1)
例:y=10000;
while(y>0)
y--;
该程序段的时间复杂度就是O(1)
时间复杂度按数量级递增排列依次为:常数阶O(1)、对数阶O(log2n)、线性阶O(n)、线性对数阶O(nlog2n)、平方阶O(n^2)、立方阶O(n^3)、……k次方阶O(n^k)、指数阶O(2^n)。
真题选解
(例题·填空题)1、下面程序段的时间复杂度为___________。
sum=1;
for(i=0;sum<n;i++)
sum+=1;
(例题·填空题)2、估算算法时间复杂度时考虑的问题规模通常是指算法求解问题的_________。
(例题·单选题)3、若一个算法的时间复杂度用T(n)表示,其中n的含义是( )
A.问题规模
B.语句条数
C.循环层数
D.函数数量
3、空间复杂度:
是某个算法的空间耗费,它是该算法所求解问题规模n的函数。
4、算法复杂度:
算法的时间复杂度和空间复杂度合称算法复杂度。
本章小结
本章的主要概念包括:数据、数据元素、数据结构、逻辑结构、存储结构;算法、
算法设计、算法分析、时间复杂度等。
算法分析是本章的一个重点,也是一个难点。要深刻理解和掌握算法分析的思想、方法以及时间复杂度的度量等概念。












