第四节 选择排序

一、直接选择排序

1、排序思想

直接选择排序(Straight Select Soft，)是一种简单的排序方法。它的基本思想是：每次从待排序的无序区中选择出关键字值最小的记录，将该记录与该区中的第一个记录交换位置。初始时，R[1…n]为无序区，有序区为空。第一趟排序是在无序区R[1…n]中选出最小的记录，将它与R[1]交换，R[1]为有序区；第二趟排序是在无序区R[2…n]中选出最小的记录与R[2]交换，此时R[1…2]为有序区；依此类推，做n-1趟排序后，区间R[1…n]中记录递增有序。

2、实例分析

【例】一组关键字(38，33，65，82，76，38，24，11)，直接选择排序过程。

3、算法描述

void SelectSort(seqList R，int n)

{　//对R作直接选择排序

　int i，j，k；

　for(i=1；i<n；i++) 　　　　　　　　　　　//做n-1趟排序

　　{　k=i；　　　　　　　　　　　　　　 //设k为第i趟排序中关键字最小的记录位置

　　　 for(j=i+1；j<=n；j++)　　　　　　　 //在[i．．n]选择关键字最小的记录

　　　　　if(R[j].key<R[k].key)

　　　　　k=j；　　　　　　　　　　　　 //若有比R[k].key小的记录，记住该位置

　　　if(k!=i)　　　　　　　　　　　　　　 //与第i个记录交换

　　　　{　R[0]=R[i]；R[i]=R[k]；R[k]=R[0]；

　　　　｝

　　｝

｝

4、算法分析

（1）时间复杂度

无论文件初始状态如何，在第i趟排序中选出最小关键字的记录需要做n-i次比较，总比较次数为（n-1）+（n-2）+…+1=n（n-1）/2；

当初始文件为正序时，移动次数为0；文件初态为反序时，每趟排序均要执行交换操作，每次交换需要移动3次，总的移动次数取最大值3（n-1）。

直接选择排序的平均时间复杂度为O(n²)。

（3）空间复杂度

直接选择排序的空间复杂度是O（1），是一个就地排序。

（4）稳定性

直接选择排序是不稳定的。

【例】假设采用不带头结点的单链表作为存储结构，试编写一个直接选择排序(升序)的算法。

设单链表结点类型和链表类型的定义如下：

typedef struct node{　　　　　　//结点类型定义

　　DataType data；　　　　　//结点数据域

　　Struct node 　*next；　　　//结点指针域

}ListNode；

typedef ListNode *LinkList；

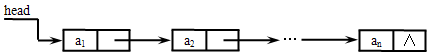
（1）按直接选择排序算法思想，交换结点的数据域和关键字域值的算法。

void Lselectsort1(Linklist head)

{　//先找最小的和第一个结点交换，再找次小的和第二个结点交换，…，以此类推

　ListNode *p，*r，*s；

　ListNode q；p=head；

　while（p!=NULL） 　　　　　　　　　　　//假设链表不带头结点

　　｛ s=p；　　　　　　　　　　　　　　 //s为保存当前关键字最小结点地址指针

　　　 r=p->next；

　　　while(r!=NULL)　　　　　　　　　　 //向后比较，找关键字值最小的结点

　　　　{ if（r->data<s->data）　　　　　　 //若r指向结点的关键字值小，使s指向它

　　　　　　s=r；

　　　　　r=r->next；　　　　　　　　　　 //比较下一个

　　　　｝

　　if（s!=p）　　　　　　　　　　　　　 //说明有关键字值比s的关键字值小的结点，需交换

　　｛ q=(*p);　　　　　　　　　　　　　 //整个结点记录赋值

　　　 p->data=s->data；

　　　 s->data=q.data；

　　　}

　　p=p->next；　　　　　　　　　　　　 //指向下一个结点

　｝

｝

（2）按直接选择排序算法思想，每次选择到最小的结点后，将其脱链并加入到一个新链表中，这样可避免结点域值交换，最后将新链表的头指针返回。

LinkList LselectSort2（LinkList head）

｛　//找最小的为新表的第一个结点，找次小的作为第二个结点，…，依次类推

　　ListNode *p，*q，*r，*s，*t，*t1；

　　t=NULL 　　　　　　　　　　　　　　　//置空表，采用尾插法建立新链表

　　while（head!=NULL）

　　　{ s=head；　　　　　　　　　　　　　 //先假设s指向关键字最小值的结点

　　　　p=head； q=NULL； 　　　　　　　 //q指向p的前趋结点

　　　　r=NULL； 　　　　　　　　　　　　//r指向s的前趋结点

　　　　while(p!=NULL)

　　　　　{ if(p->data <s-> data)　　　　　　　　　 //使s指向当前关键字值小的结点

　　　　　　　{s=p；r=q；　　　　　　　　 //使r指向s的前一个结点

　　　　　　　｝

　　　　　　q=p； p=p->next； 　　　　　　//指向后继结点

　　　　　}

　　　　if(s==head) 　　　　　　　　　　　//没发现更小的

　　　　　head=head->next；　　　　　　　 //删除第一个结点

　　　　else

　　　　　r->next=s->next；　　　　　　　 //删除最小结点

　　　　if(t==NULL)

　　　　　{t=s；t1=t；)　　　　　　　　　 //t1指向新表的当前尾结点

　　　　else 　　　　　　　　　　　　　　//插入新结点

　　　　　{ t1->next=s； t1=s; }

　　　　　}

　　　t1->next=NULL；

　　　return t; 　　　　　　　　　　　　　　//返回新表头指针

}

1、堆排序定义

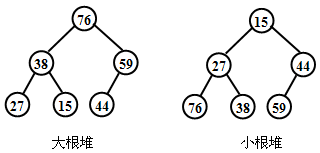
n个关键字序列K_l，K₂，…，K_n称为堆，当且仅当该序列满足如下关系：

（1） ki≤K_2i且k_i≤K_2i+1 或（2）K_i≥K_2i且k_i≥K_2i+1(1≤i≤ )

前者称为小根堆，后者称为大根堆。

【例】关键字序列(76，38，59，27，15，44)就是一个大根堆，还可以将此调整为小根堆(15，27，44，76，38，59)，它们对应的完全二又树如图：

2、堆排序的思想

从小到大排序的步骤：

第一步：将参加排序的原始序列转换为第一个大根堆（建初始堆）。

第二步：把堆的第一个元素（最大值元素）与堆的最后那个元素交换位置。

第三步：将在第二步中"去掉"最大值元素后剩下的元素组成的序列重新调整为一个新的堆。

第四步：重复第二步与第三步n-1次，直到排序结束。

3、实例分析

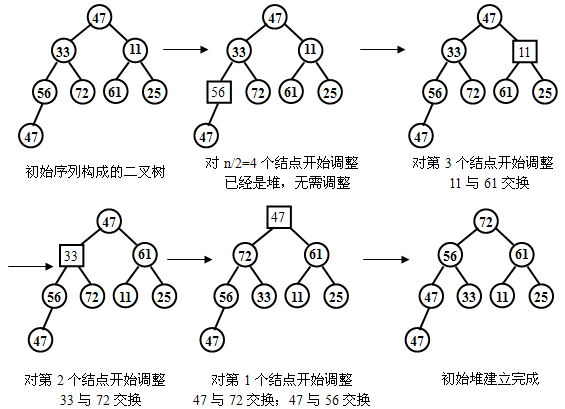
【例】已知关键字序列为(47，33，1l，56，72，61，25，47)，采用堆排序方法对该序列进行堆排序，画出建初始堆的过程和每一趟排序结果。

第一步：将参加排序的原始序列转换为第一个大根堆（建初始堆）。

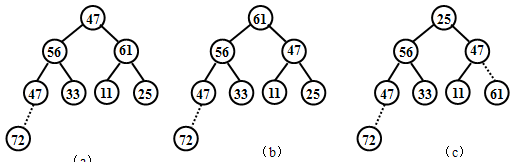
第二步：将根结点（最大值）与最后一个结点调换如下图（a）所示，完成第一趟排序，第一趟排序的结果为：47　56 　61 　47 　33 　11 　25　 [72]

第三步，将第一趟排序的结果除最后一个元素外的其余结点组成的序列调整为堆，如图（b）所示，然后将根结点与倒数第2个结点调换如下图（c）所示，完成第二趟排序，第二趟排序的结果为：25　 56　 47　 47　 33　 11　 25　 [61 　72]

第四步，将第二趟排序的结果除最后2个元素外的其余结点组成的序列调整为堆，如图（d）所示，然后将根结点与倒数第3个结点调换如下图（e）所示，完成第三趟排序，第三趟排序的结果为：11　 47　 47 　25　 33　 [56　 61　 72]

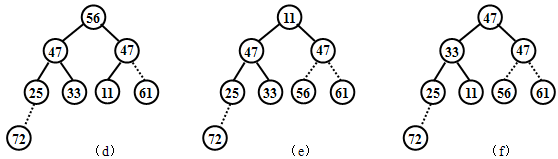
第五步，将第三趟排序的结果除最后3个元素外的其余结点组成的序列调整为堆，如图（f）所示，然后将根结点与倒数第4个结点调换如图（g）所示，完成第四趟排序，第四趟排序的结果为：11　 33　 47　 25　 [47　 56　 61　 72]

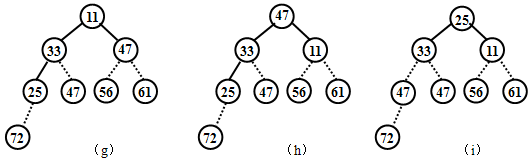
第六步，将第四趟排序的结果除最后4个元素外的其余结点组成的序列调整为堆，如图（h）所示，然后将根结点与倒数第5个结点调换如图（i）所示，完成第五趟排序，第五趟排序的结果为：25　 33　 11　 [47　 47 　56 　61 　72]

第七步，将第五趟排序的结果除最后5个元素外的其余结点组成的序列调整为堆，如图（j）所示，然后将根结点与倒数第6个结点调换如图（k）所示，完成第六趟排序，第六趟排序的结果为：11　 25　 [33　 47　 47　 56　 61　 72]

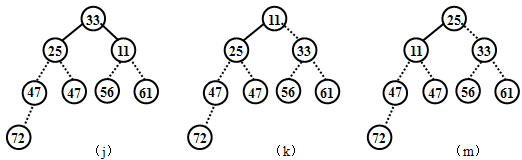
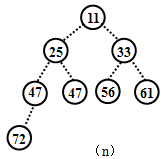
第八步，将第六趟排序的结果除最后6个元素外的其余结点组成的序列调整为堆，如图（m）所示，然后将根结点与倒数第7个结点调换如图（n）所示，完成第七趟排序，第七趟排序的结果为：11　 [25　 33 　47　 47　 56　 61 　72] 。排序结束（8个元素七趟排序）。

4、算法分析

堆排序方法是一种不稳定的排序方法，具有n个数据元素的序列，堆排序方法的排序趟数为n-1，其时间复杂度为O（nlog₂n），空间复杂度为O（1）。