第三节　线性表的链式存储结构（四）

循环链表与单链表的区别仅仅在于其尾结点的链域值不是NULL，而是一个指向头结点的指针。

循环链表的主要优点是：从表中任意一结点出发都能通过后移操作而遍历整个循环链表。

在循环链表中，将头指针改设为尾指针（rear）后，无论是找头结点、开始结点还是终端点都很方便，它们的存储位置分别是rear->next、rear->next->next和rear，这样可以简化某些操作。

例：已知有一个结点数据域为整型的，且按从大到小顺序排列的头结点指针为L的非空单循环链表，试写一算法插入一个结点(其数据域为x)至循环链表的适当位置，使之保持链表的有序性。

分析：要解决这个算法问题，首先就是要解决查找插入位置，方法：使用指针q扫描循环链表，循环条件应该是（q->data>x&&q!=L），同时使用指针p记录q的直接前驱，以方便进行插入操作。

算法描述

voidInsertList(LinkList L，int x)

｛ //将值为x的新结点插入到有序循环链表中适当的位置

　　ListNode *s，*p，*q;

　　s=(ListNode *)malloc(sizeof(ListNode))； 　　　　　　　//申请结点存储空间

　　s->data=x; p=L；

　　q=p->next; 　　　　　　　　　　　　　　　　　　　//q指向开始结点

　　while(q->data>x&&q!=L)　　　　　　　　　　　　　 //查找插入位置

　　　{ p=p->next;　　　　　　　　　　　　　　　　　 //p指向q的前趋结点

　　　　q=p->next;　　　　　　　　　　　　　　　　　 //q指向当前结点

　　　}

　　p->next=s；　　　　　　　　　　　　　　　　　　 //插入*s结点

　　s->next=q；

}

算法分析：

①该算法在最好情况下，也就是插入在第一个结点前面，循环一次也不执行；

②在最坏情况下，即插在最后一个结点之后，当循环需要执行n次；

③该算法的时间复杂度为O (n)。

真题选解

四、双向链表

双向循环链表示意图

双向链表结点

双向链表及其结点的类型描述

typedef struct dlnode

{ DataType data；

　struct 　dlnode 　*prior，*next；

｝DLNode； //双向链表结点的类型定义

typedef 　DLNode 　*DLinkList；

DlinkList head； //head为指向双向链表的指针

双链表结构是一种对称结构，既有前向链，又有后向链，这就使得插入操作及删除操作都非常方便。设指针p指向双链表的某一结点，则双链表结构的对称性可用下式来描述：

p->prior ->next==p->next->prior==p

在双链表上实现求表长、按序号查找、定位、插入和删除等运算与单链表上的实现方法基本相同，不同的主要是插入和删除操作。

1、删除操作。

删除双链表中p所指结点

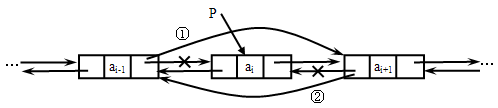
分析：操作过程如图所示

① p ->prior ->next=p->next；② p ->next ->prior=p->prior；

算法描述

DataType DLDelete(DLNode *p)

{ //删除带头结点的双向链表中指定结点*p

　p->prior->next=p->next；

　p->next->prior=p->prior; //上面两条语句的顺序可以调换，不影响操作结果。

　x=p->data;

　free(p)；

　return x；

}

算法分析：算法的时间复杂度为O（1）

2、插入操作：

将值为x的新结点插入到带头结点的双向链表中指定结点*p之前。

分析：操作过程如图所示

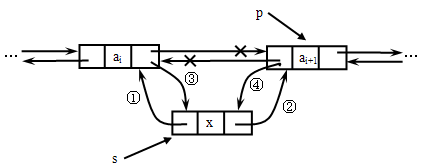
算法描述

void DLInsert(DLNode *p，DataType x)

{ //将值为x的新结点插入到带头结点的双向链表中指定结点*p之前

　DLNode *s=(DLNode*)malloc(sizeof(DLNode))；　　 //申请新结点

　s->data=x；

　s->prior=p->prior；　　　　　　　　　　　　　　 //完成①步操作

　s->next=p; 　　　　　　　　　　　　　　　　　　//完成②步操作

　p->prior->next=s; 　　　　　　　　　　　　　　　//完成③步操作

　p->prior=s；　　　　　　　　　　　　　　　　　 //完成④步操作

}

算法分析：算法的时间复杂度为O（1）

补充：在p所指结点的后面链入一个新结点*s，则需修改四个指针：

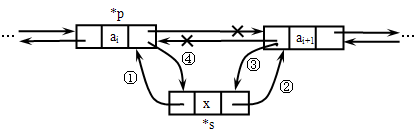
① s->prior= p； ② s->next=p->next；

③ p->next->prior=s； ④ p->next=s；

注：③和④两条语句的顺序不能调换，否则操作结果错误。

下面四条语句也可以完成插入操作。

① s->prior=p； ② s->next=p->next；

③ p->next=s； ④ s->next->prior=s；

真题选解

例：假设有一个头结点指针为head的循环双向链表，其结点类型结构包括三个域：prior、data和next。其中data为数据域，next为指针域，指向其后继结点，prior也为指针域，其值为空(NULL)，因此该双向链表其实是一个单循环链表。试写一算法，将其表修改为真正的双向循环链表。

分析：链表初始状态如下图所示

修改后的链表如下图所示

方法：以p指向头结点开始，循环使用语句p->next->prior=p；和p=p->next；即可实现题目要求。

算法描述

void trans(DLinkList head)

{

　DLNode *p；

　p=head； //使p指向头结点

　while(p->next!=head)　　　　　 //依次从左向右，对每个结点的prior赋值

　　 { p->next->prior=p；　　　　 //p所指结点的直接后继结点的前趋就是p

　　　p=p->next； 　　　　　　//p指针指向下一个结点

　　}

　head->prior=p； 　　　　　　// head的前趋指向表的终端结点

｝

算法分析：算法要从头至尾扫描两个链表，算法的时间复杂度是O（n）