第二节 - 栈的应用举例
发布时间：2020-09-20 10:39来源：未知
第二节 栈的应用举例
一、圆括号匹配的检验
对于输入的一个算术表达式字符串，试写一算法判断其中圆括号是否匹配，若匹配则返回TRUE，否则返回FALSE。
【分析】利用栈的操作来实现：循环读入表达式中的字符，如遇左括号"("就进栈；遇右括号")"则判断栈是否为空，若为空，则返回FALSE，否则退栈；循环结束后再判断栈是否为空，若栈空则说明括号匹配，否则说明不匹配。
【算法描述】
int Expr( )
{ SeqStack S；
DataType ch，x；
InitStack(&S); //初始化栈S
ch=getchar();
while(ch!='\n')
{ if(ch=='(')
Push(&S，ch)； //遇左括号进栈
else
if(ch==')')
if(StackEmpty(&S)) //遇右括号如果栈空，说明不匹配，返回0
return 0;
else
x=Pop(&s)； //遇右括号退栈
ch=getchar(); //读入下一个字符
}//end of while
if(StackEmpty(&S)) return 1; //最后栈空，说明匹配，返回1
else return 0；
}
二、字符串回文的判断
利用顺序栈的基本运算，试设计一个算法，判断一个输入字符串是否具有中心对称(也就是所谓的"回文"，即正读和反读均相同的字符序列)，例如ababbaba和abcba都是中心对称的字符串。
【分析】从中间向两头进行比较，若完全相同，则该字符串是中心对称，否则不是。这就要首先求出字符串串的长度，然后将前一半字符入栈，再利用退栈操作将其与后一半字符进行比较。
【算法描述】
int symmetry(char str[ ])
{ SeqStack S；
int j，k，i=0；
InitStack(&S)；
while(Str[i]!='\0') i++; //求串长度
for(j=0；j<i/2；j++)
Push(&s，str[j])； //前一半字符入栈
k=(i+1)／2; //后一半字符在串中的起始位置
//特别注意这条命令怎么处理奇偶数个字符的。
for(j=k；j<i；j++) //后一半字符与栈中字符比较
if(str[j]!=Pop(&s))
return 0； //有不相同字符，即不对称
return 1； //完全相同，即对称
}
三、数制转换
将一个非负的十进制整数N转换成d进制
【分析】将一个非负的十进制整数N转换成d进制的方法：N除以d，求出每一步所得的余数，然后将所有余数逆序书写就是十进制整数N对应的d进制数。
例如（3553）10=（6741）8，其运算过程如下：
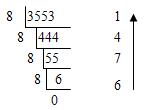
【算法描述】
void conversion(int N，int d)
{ //将一个非负的十进制数N转换成任意的d进制数
SeqStack S；
InitStack(&S)
while(N)
{ Push(&S，N％d)； //N除以d的余数入栈
N=N／d； //N除以d的商
}
while(!StackEmpty(&S))
{ i=Pop(&S)；
printf("％d"，i)； //出栈完成余数倒序输出
}
}
四、栈与递归
栈还有一个非常重要的应用就是在程序设计语言中实现递归。一个直接调用自己或间接调用自己的函数，称为递归函数。
递归是程序设计中一个强有力的工具，递归算法有两个关键条件：一是有一个递归公式；二是有终止条件。
例如：求n的阶乘可递归地定义为
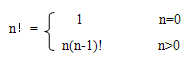
2阶的Fibinocci数列：
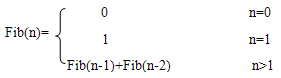
【例】试分析求阶乘的递归函数。
【算法描述】
long int fact(int n)
{ int temp;
if(n==0)
return 1; //递归终止条件
else
temp=n*fact(n-1); //递归公式
r12：return temp;
}
void main() //主函数
{ long int n;
n=fact(5); //调用fact()函数求5！
r11：printf("5!=％ld"，n)；
}
【算法分析】
| 调用层次 | 调用 | 参数n | 返回地址 | temp结果 | 退栈时计算结果 |
| ↑5 | fact(0) | 0 | r12 | 1 | ↓ |
| ↑4 | fact(1) | 1 | r12 | 1* fact(0) | 1*1=1↓ |
| ↑3 | fact(2) | 2 | r12 | 2*fact(1) | 2*1=2↓ |
| ↑2 | fact(3) | 3 | r12 | 3*fact(2) | 3*2=6↓ |
| ↑1 | fact(4) | 4 | r12 | 4*fact(3) | 4*6=24↓ |
| ↑0 | fact(5) | 5 | r11 | 5*fact(4) | 5*24=120返回 |
| 进栈 | 主函数打印5！=120 退栈 | ||||
【例】已知函数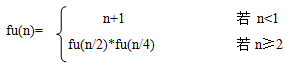
，试写一个递归算法，实现其功能。
【算法描述】
float fu(int n)
{ if(n<2)
return (n+1)； //递归终止条件
else
return fu(n/2)*fu(n/4); //递归公式
}
或者为
float fu(int n)
{ float f1，f2j
if(n<2)
return (n+1)；
else
{ f1=fu(n/2)；
f2=fu(n/4)；
return(f1*f2)；
}
}
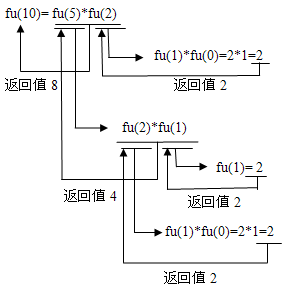
假设有主函数
main()
{ int n=10；
printf("fu()=％f＼n"，fu(n));
}
其调用和执行过程
