第一节 - 多维数组和运算
发布时间:2020-09-20 10:43来源:未知
第一节 多维数组和运算
一、多维数组的定义
1、一维数组
是一种元素个数固定的线性表。
2、多维数组
是一种复杂的数据结构,可以看成是线性表的推广,一个n维数组可视为其数据元素为n-1维数组的线性表。
二、数组的顺序存储
通常采用顺序存储结构来存放数组。对二维数组可有两种存储方法:一种是以行序为主序的存储方式,另一种是以列序为主序的存储方式。在C语言中,采用以行为主序存储。
(1)对于C语言的二维数组A[m][n],下标从0开始,假设一个数组元素占d个存储单元,则二维数组中任一元素a[i][j]的存储位置可由下式确定:
loc(A[i][j])=loc(A[0][0])+(i *n + j) * d
【真题选解】
(例题·单选题)二维数组A[4][5]按行优先顺序存储,若每个元素占2个存储单元,且第一个元素A[0][0]的存储地址为1000,则数组元素A[3][2]的存储地址为( )
A.1012
B.1017
C.1034
D.1036
(2)对于C语言的三维数组A[m][n][p],下标从0开始,假设一个数组元素占d个存储单元,则三维数组中任一元素a[i][j][k]的存储位置可由下式确定:
loc(A[i][j][k])=loc(A[0][0][0]+(i *n *p+ j*p+k) * d
(例题·单选题)三维数组A[4][5][6]按行优先存储方法存储在内存中,若每个元素占2个存储单元,且数组中第一个元素的存储地址为120,则元素A[3][[4][5]的存储地址为( )。
A.356
B.358
C.360
D.362
三、数组运算举例
【例】设计一个算法,实现矩阵Amn的转置矩阵Bnm。
【分析】对于一个m×n的矩阵A,其转置矩阵是一个n×m的矩阵B,而且B[i][j]=A[j][i],0≤i≤n-1,0≤j≤m-1。假设m=5,,n=8。
【算法描述】
void trsmat(int a[][8],int b[][5],int m,int n)
{ int i,j;
for(j=O;j<m;j++)
for(i=0;i<n;i++)
b[i][j]=a[j][i];
}
【例】如果矩阵A中存在这样的一个元素A[i][j],满足:A[i][j]是第i行元素中最小值,且又是第j列元素中最大值,则称此元素为该矩阵的一个马鞍点。假设以二维数组存储矩阵Am×n,试编写求出矩阵中所有马鞍点的算法。
【分析】算法思想:先求出每行中的最小值元素,存入数组Min[m]之中,再求出每列的最大值元素,存入数组Max[n]之中。若某元素既在Min[i]中又在Max[j]中,则该元素A[i][j]就是马鞍点,找出所有这样元素。
【算法描述】
void MaxMin(int A[4][5],int m,int n)
{ int i,j;
int Max[5],Min[4];
for(i=O;i<m;i++) //计算每行的最小值元素,存入Min数组中
{ Min[i]=A[i][O]; //先假设第i行第一个元素最小,然后再与后面的元素比较
for(j=1; j<n;j++)
if (A[i][j]<Min[i])
Min[i]=A[i][j];
}
for(j=0;j<n;j++) //计算每列的最大值元素,存入Max数组中
{ Max[j]=A[O][j]; //假设第j列第一个元素最大,然后再与后面的元素比较
for(i=1; i<m; i++)
if(A[i][j]>Max[j])
Max[j]=A[i][j];
}
for(i=0;i<m; i++)
for (j=0;j<n; j++)
if(Min[i]==Max[j]) //判断是否为马鞍点
printf("(%d,%d", i,j); //显示马鞍点
}
【真题选解】
(例题·算法阅读题)阅读下列程序。
void f30(int A[],int n)
{ int i,j,m;
for(i=1;i<n;i++)
for(j=0;j<i;j++)
{ m=A[i*n+j]; // A[i*n+j]与A[j*n+i]值交换
A[i*n+j]=A[j*n+i];
A[j*n+i]=m;
}
}
回答下列问题:
(1)已知矩阵 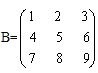 ,将其按行优先存于一维数组A中,给出执行函数调用f30(A,3)后矩阵B的值;
,将其按行优先存于一维数组A中,给出执行函数调用f30(A,3)后矩阵B的值;
(2)简述函数f30的功能。












