第三节 - 广义表基础
发布时间:2020-09-20 10:45来源:未知
第三节 广义表基础
一、广义表的定义
广义表是线性表的推广。即广义表中放松对表元素的原子限制,容许它们具有其自身结构。
1、广义表定义
广义表是n(n≥0)个元素a1,a2,…,ai,…,an的有限序列。
其中:
①ai--或者是原子或者是一个广义表。
②广义表通常记作:
Ls=( a1,a2,…,ai,…,an)。
③Ls是广义表的名字,n为它的长度。
④若ai是广义表,则称它为Ls的子表。
⑤一个表展开后所含括号的层数称为广义表的深度
注意:
①广义表通常用圆括号括起来,用逗号分隔其中的元素。
②为了区分原子和广义表,书写时用大写字母表示广义表,用小写字母表示原子。
③若广义表Ls非空(n≥1),则al是LS的表头(head),其余元素组成的表(a1,a2,…,an)称为Ls的表尾(tail)。
④广义表是递归定义的
【例】
(1)A=()--A是一个空表,其长度为零,深度为1。
(2)B=(a)--B是一个只有一个原子的广义表,其长度为1,深度为1。
(3)C=(a,(b,c))--C是一个长度为2的广义表,第一个元素是原子,第二个元素是子表,深度为2。
(4)D=(A,B,C)=((),(a),(a,(b,c)))--D是一个长度为3的广义表,其中三个元素均为子表,深度为3。
(5)E=(C,d)=((a,(b,c)),d)--E是一个长度为2的广义表,第一个元素是子表,第二个元素是原子,深度为3。
(6)F=(e,F)=(e,(e,(e,…)))--F是一个递归的表,它的长度为2,第一个元素是原子,第二个元素是表自身,展开后它是一个无限的广义表,深度为∞。
2、广义表的几个重要性质:
(1)广义表的元素可以是子表,而子表又可以含有子表,因此广义表是一个多层次结构的表,它可以用图来形象地表示。
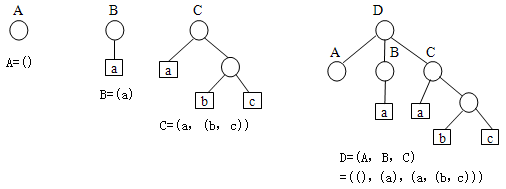
(2)广义表具有递归和共享的性质,例如,表F就是一个递归的广义表,D表是共享的表,在表D中可以不必列出子表的值,而是通过子表的名字来引用。
二、广义表的基本运算
广义表是对线性表和树的推广, 广义表的大部分运算与这些数据结构上的运算类似。 在此,只讨论广义表的两个特殊的基本运算:取表头head(Ls)和取表尾tail(Ls)。任何一个非空的广义表其表头可能是原子,也可能是子表,而其表尾一定是子表。
【例】已知有下列的广义表,试求出下面广义表的表头head()、表尾tail()、表长length()和深度depth()。
(1)A=(a,(b,c,d),e,(f,g)); (2)B=((a));
(3)C=(y,(z,w),(x,(z,w),a)); (4)D=(x,((y),B),D)。
【例】取出广义表A=((x,y,z),(a,b,c,d))中原子b的函数是__________。
真题选解
(例题·填空题)1、已知广义表如下:
A=(B,y) B=(x,L) L=(a,b)
要求:
(1)写出下列操作的结果
tail(A)=_______________.
head(B)=______________。
(2)请画出广义表A对应的图形表示。
(例题·填空题)2、已知广义表C=(a,(b,c),d),则:tail(head(tail(C)))= _________。
三、广义表的存储结构
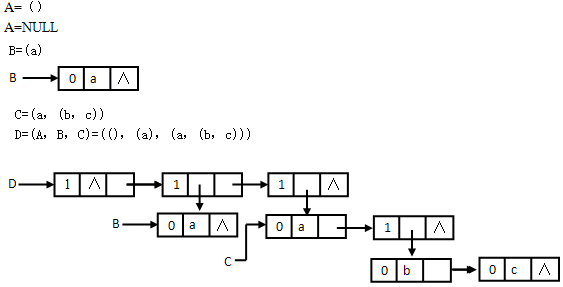
1、结点结构
![]()
说明:(1)tag标志位,tag=1,该结点是子表,第二个域为slink,用以存放子表的地址;当tag=0时,该结点是原子结点,第二个域为data,用以存放元素值。
(2)link域是用来存放与本元素同一层的下一个元素对应结点的地址,当该元素是所在层的最后一个元素时,link的值为NULL。
【例】
运算的实现考试大纲没做要求,不讲。
本章小结
前两章讨论的线性表、栈和队列都是典型的线性结构,结构中数据元素都是不能分解的非结构的原子类型。它们的逻辑特征是:每个数据元素至多有一个直接前趋和直接后续。而多维数组和广义表是一种复杂的非线性结构,它们的逻辑特征是:一个数据元素可能有多个直接前趋和直接后继。
多维数组可以看成是线性表的推广。因为一旦确定数组是按行或按列优先顺序存储之后,每个数组元素之间的关系就同一维数组一样变成线性的了。因此,只要弄清楚多维数组按行优先顺序存储结构之后,它的运算就同线性表的运算类似。
本章主要介绍数组的逻辑结构特征及其存储方法、特殊矩阵和稀疏矩阵的压缩存储方法,压缩存储特殊矩阵和稀疏矩阵的各种运算及应用。以及广义表的逻辑结构、表的表头及表尾的求解。












