第三节 - 二叉树的运算
发布时间:2020-09-20 10:49来源:未知
第三节 二叉树的运算
一、二叉树的生成
1.按广义表表示二叉树结构生成二叉链表的算法
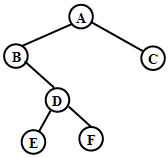
上图所示二叉树的广义表表示形式为: (A(B(,D(E,F)),C))。特点:靠近左括号的结点是在左子树上,而逗号右边的结点是在右子树上。
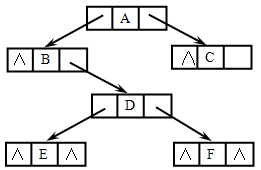
算法中用了一个指针数组来模拟栈存储结点的双亲指针,根据读入广义表中的字符分四种不同的情况进行处理:
【算法描述】
BinTNode * CreateTree(char * str)
{ //str为存储广义表的字符串的指针
BinTNode *st[100]; //用指针数组模拟栈
BinTNode *p=NULL;
int top,k,j=0;
top= -1; //置空栈
char ch=str[j]; //存放广义表的字符串的数组
BinTNode *b=NULL;
while(ch!='\0') //循环读广义表字符串中字符
{ switch(ch)
{ case '(':top++;st[top]=p;k=1;break;
//左括号表示新的子树的开始,所以刚建立的结点指针入栈
case ')':top--;break;
//右括号表示一个子树的结束,栈顶元素没有子树,出栈
case ',':k=2;break;
default:p=(BinTNode*)malloc(sizeof(BinTNode));//读到的是字符
p->data=ch ; //填写数据域
p->lchild=p->rchild=NULL; //填写指针域
if(b==NULL) //建立第一个结点
b=p;
else
{ switch(k)
{ case 1:st[top]->lchild=p; break;
//前一个字符是'(',该结点应该插入到左子树
case 2:st[top]->rchild=p;break;
//前一个字符是','该结点应该插入到右子树
}
}
}
j++; ch=str[j]; //读取下一个字符
}
return b; //返回根结点的指针
}
2.按完全二叉树的层次顺序依次输入结点信息建立二叉链表的算法
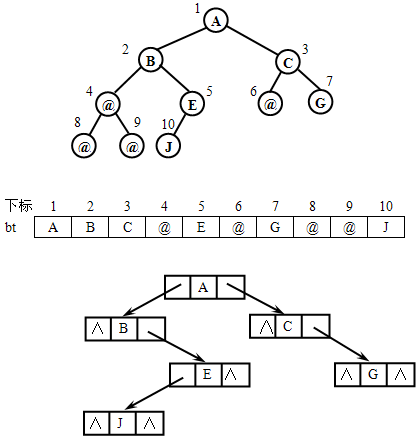
【算法思想】首先对一般的二叉树添加若干个虚结点,使其成为完全二叉树,然后依次输入结点信息,若输入的结点不是虚结点"@",则建立一个新结点,若是第一个结点,则令其为根结点,否则将新结点作为左孩子或右孩子链接到它的双亲结点上。如此重复下去,直到输入结束符号"#"时为止(假设结点数据域为字符型)。
【算法描述】
BinTree CreateBinTree(BinTree bt)
{ //Q[1..n]是一个BinTNode类型的指针数组,front和rear分别是队头和队尾指针
BinTNode *Q[100]; //定义队列
BinTNode *s;
int front,rear; char ch;
ch=getchar( );bt=NULL; //置空二叉树
front=1;rear=0; //初始化队列
while(ch!='#') //假设结点值为单字符,#为终止符。
{ s=NULL; //先假设读入的为虚结点"@"
if(ch!='@')
{s=(BinTNode*)malloc(sizeof(BinTNode)); //申请新结点
s->data=ch; s->lchlid=s->rchiId=NULL; //新结点赋值
}//endif_1
rear++; //队尾指针自增
Q[rear]=s; //将新结点地址或虚结点地址(NULL)入队
if(rear==1) //若rear为1,则说明是根结点,用bt指向它
bt=s;
else
{if(s!=NULL&&Q[front]!=NULL)
//当前结点及其双亲结点都不是虚结点
if(rear%2==0) //rear为偶数,新结点应作为左孩子
Q[front]->lchild=s;
e1se //rear为奇数,新结点应作为右孩子
Q[front]->rchild=s ;
if(rear%2!=0)
front++; //rear为奇数,说明front所指结点的左右儿子都处理完了,因此front加1指向下一个双亲
}
ch=getchar(); //读下一个结点值
}//endwhile
return bt;
}
二、二叉树的遍历
遍历:是指沿着某条搜索路径(线)周游二叉树,依次对树中每个结点访问且仅访问一次。
遍历方案
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
①访问根结点本身(D),
②遍历根结点的左子树(L),
③遍历根结点的右子树(R)。
以上三种操作有六种执行次序:
DLR(根左右)、LDR(左根右)、LRD(左右根);
DRL(根右左)、RDL(右根左)、RLD(右左根)。
注意:前三种次序与后三种次序对称,故只讨论先左后右的前三种次序。
1、递归遍历算法
三种遍历的递归定义:
(1)先序遍历DLR(根左右):也叫先根遍历,若二叉树非空,则依次执行如下操作:
① 访问根结点; ②遍历左子树;③遍历右子树。
(2)中序遍历LDR(左根右):也叫中根遍历,若二叉树非空,则依次执行如下操作:
①遍历左子树; ②访问根结点; ③遍历右子树。
(3)后序遍历LRD(左右根):也叫后根遍历,若二叉树非空,则依次执行如下操作:
①遍历左子树; ②遍历右子树; ③访问根结点。
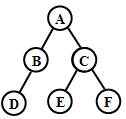
【例】分别写出图所示的二叉树的前序、中序、后序遍历序列。
【答案】
前序遍历序列:ABDCEF
中序遍历系列:DBAECF
后序遍历序列:DBEFCA
【真题选解】
(例题•分析题)假设二叉树的RNL遍历算法定义如下: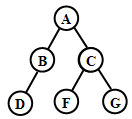
若二叉树非空,则依次执行如下操作:
(1)遍历右子树;
(2)访问根节点;
(3)遍历左子树。
已知一棵二叉树如图所示,请给出其RNL遍历的结果序列。
三种遍历的算法
(1)前序遍历递归算法
void Preorder(BinTree bt)
{ //采用二叉链表存储结构,并设结点值为字符型
if(bt!=NULL)
{ printf("%c",bt->data); //访问根结点
Preorder(bt->lchild); //前序遍历左子树
preorder(bt->rchild); //前序遍历右子树
}
}
(2)中序遍历递归算法
void Inorder(BinTree bt)
{ if(bt!=NULL)
{ Inorder(bt->lchild); //中序遍历左子树
printf("%c",bt->data); //访问根结点
Inorder(bt->rchild); //中序遍历右子树
}
}
(3)后序遍历递归算法
void Postorder(BinTree bt)
{ if(bt!=NULL)
{ Postorder(bt->lchild); //中序遍历左子树
Postorder(bt->rchild); //中序遍历右子树
printf("%c",bt->data); //访问根结点
}
}
2、二叉树遍历的非递归算法
(1)利用栈的非递归中序遍历算法:
void Inorderl(BinTree bt)
{ // 采用二叉链表存储结构
SeqStack S;BinTNode *P;
InitStack(&S);
Push(&S,bt); //根结点入栈
while(!StackEmpty(&S))
{ while(GetTop(&S)) //读栈顶元素,当栈顶不为空
Push(&S,GetTop(&S)->lchild); //左孩子依次入栈,直到左子树空为止
p=Pop(&S); //最后一个入栈的空指针退栈
if(!StackEmpty(&S))
{ printf("%c",GetTop(&S)->data); //访问根结点
p=Pop(&S);
Push(&S,p->rchild); //右子树进栈
}
}
}
(2)利用指针数组模拟栈实现的非递归中序遍历算法:
void Inorder2(B1nTree bt)
{ //二叉树非递归中序遍历算法
BinTNode *ST[100]; //用指针数组模拟栈
int top=0; //初始化数组
ST[top]=bt;
do
{ while(ST[top]!=NULL) //根结点及其所有的左结点地址装入数组
{ top=top+1;
ST[top]=ST[top-1]->lchild;
}
top=top-1; //最后一个入数组的空指针退"栈"
if(top>=0) //判数组中地址是否访问完
{ printf("%c",ST[top]->data); //访问结点
ST[top]=ST[top]->rchild; //扫描右子树
}
}while(top!=-1);
}
(3)利用栈的非递归前序遍历算法。
算法思想:利用栈先将二叉树根结点指针入栈,然后执行出栈,获取栈顶元素值(即结点指针),若不为空值,则访问该结点,再将右、左子树的根结点指针分别入栈,依次重复出栈、入栈,直至栈空为止。
void Preorderl(BinTree bt)
{ SeqStack S;
InitStack(&S); //初始化栈
Push(&S,bt), //根结点指针进栈
while(!StackEmpty(&S))
{ bt=Pop(&S); //出栈
if(bt!=NULL)
{ printf("%c",bt->data); //访问结点,假设数据域为字符型
Push(&S,bt->rchild); //右子树入栈 先访问左子树,栈先进后出
Push(&S,bt->lchiid); //左子树入栈
}
}
}
(4)非递归的按层遍历二叉链表树。
按层遍历二叉树:从上到下,从左到右遍历二叉树。
【例】对下图二叉树按层进行遍历
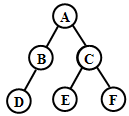
【答案】ABCDEF
算法思想:采用一队列Q,若树不空,先将二叉树根结点输出,并将根结点指针入队,然后出队。若根结点有左子树,则将左子树的根结点输出并将其指针入队;若其有右子树,则将其右子树的根结点输出并将其指针入队,再出队,如此下去,直至队列空为止。
void TransLevel(BinTree bt)
{ cirQueue Q; //按层遍历二叉树,从上到下,从左到右
InitQueue(&Q); //初始化队列为空队列
if(bt==NULL)
return;
e1se
{ printf("%c",bt->data); //输出根结点,假设其数据域为字符型
EnQueue(&Q,bt); //根结点指针入队
while(!QueueEmpty(&Q))
{ bt=DeQueue(&Q); //出队列
if(bt->rchild!=NULL)
{ printf("%c",bt->lchild->data); //输出左子树根结点
EnQueue(&Q,bt->1child); //左子树入队
}
if(bt->rchild!=NULL)
{ printf("%c",bt->rchild->data); //输出右子树根结点
EnQueue(&Q,bt->rchild); //右子树入队列
}
}//end of the while
}//end of the if
}
3、由遍历序列恢复二叉树
(多次在全国自学考试试题中出现)
(1)已知二叉树的前序遍历序列和中序遍历序列,可以唯一地恢复该二叉树。
原则是:在前序序列中确定根结点(最前面那个结点一定是根结点),然后根据根结点在中序序列中的位置分出根结点的左、右子树(根结点前面的那些结点为根结点的左子树上的结点,根结点后面的那些结点为根结点的右子树上的结点)。恢复该二叉树的任何一棵子树的过程仍然遵循这个原则。
【例】已知一棵二叉树的前序遍历序列与中序遍历序列分别为
前序遍历序列:A B C D E F G H I
中序遍历序列:B C A E D G H F I
试恢复该二叉树。
【解答】按照上述分解原则求得整棵二叉树的过程如所示。
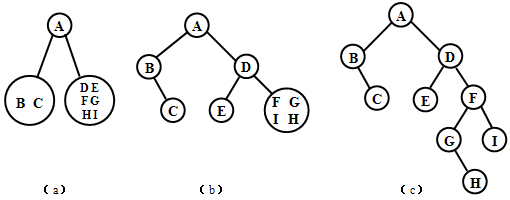
同理,已知二叉树的中序遍历序列和后序遍历序列,也可以唯一地恢复该二叉树,只是在后序序列中去确定根结点(最后面那个结点一定是根结点),而在中序序列中分出左右子树的过程与上述过程没有区别。
已知二叉树的前序遍历序列和后序遍历序列,无法唯一地恢复该二叉树,因为无法确定左右子树。
三、二叉树应用举例
【例1】已知二叉树的链式存储结构,求二叉树的深度。【真题】
【分析】若一棵二叉树为空,则它的深度为0,否则它的深度等于其左右子树中的最大深度加l。设depl和depr分别表示左右子树的深度,则二叉树的深度为:
max(depl,depr)+1
【算法描述】
int BinTreeDepth(BinTree bt)
{ int depl,depr;
if(bt==NULL)
return 0; //对于空树,返回0值,结束递归
else
{ depl=BinTreeDepth(bt->lchild); //计算左子树的深度
depr=BinTreeDepth(bt->rchild); //计算右子树的深度
if(depl>depr)
return depl+1;
else
return depr+1;
}
}
【例2】以二叉链表为存储结构,试编写在二叉树中查找值为x的结点的位置。
【分析】该算法是比较简单的,无论是利用三种遍历算法的哪一种,都很容易实现,不妨用前序遍历算法。
【算法描述】
int found=0;
BinTNode *P; //用found来作为是否查找到的标志
void FindBT(BinTree bt,DataType x)
{ BinTNode *P=NULL;
if((bt!=NULL)&&(!found))
if(bt->data==x)
{p=bt; found=l;
}
else
{ FindBT(bt->lchild,x); //遍历左子树查找x
FindBT(bt->rchild,x); //遍历右子树查找x
}
}
【例3】以二叉链表为存储结构,试编写p所指结点在树中层数的算法。
【分析】设h为返回P所指结点的所在层数,初值为0;树为空时返回0。lh指示二叉树bt的层数(即高度),调用时置初值为为l。
【算法描述】
int Level(BinTree bt,BinTNode*P,int lh)
{ //求一结点在二叉树中的层次
static int h=0: //h设置为静态遍历
if(bt==NULL) h=0;
else
if(bt==p)
h=lh;
else
{ Level(bt->lchild,p,lh+1); //左子树中查找p
if(h==O) //表示左子树已查完
Level(bt->rchild,p,lh+1); //右子树中查找p
}
return h;
}












