第四节 线索二叉树

一、线索二叉树的概念

1、定义

n个结点的二叉链表中含有n+1个空指针域。利用二叉链表中的空指针域，存放指向结点在某种遍历次序下的前趋和后继结点的指针（这种附加的指针称为"线索"）。

这种加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树。根据线索性质的不同，线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。

2、线索链表的结点结构

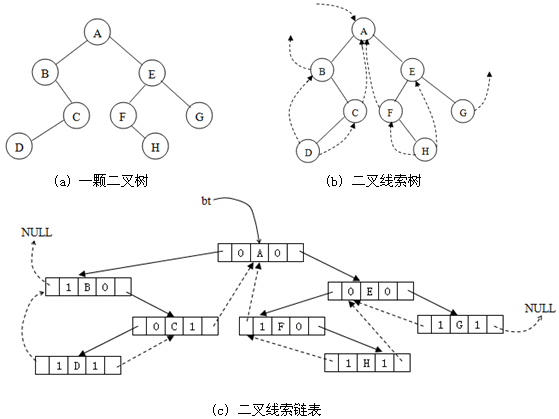
【例】如图 (a)所示的二叉树所对应的中序线索二叉树如图 (b)所示，图 (c)所示为二叉线索链表树。

3、线索链表的结点类型定义

typedef struct node

｛ DataType data；

　 int ltag，rtag；

　 struct node *lchild，*rchild；

｝ BinThrNode ；　　　　　　　　　 //线索链表结点类型

typedef BinThrNode *BinThrTree； 　　//定义线索链表类型

二、二叉树线索化算法

1、算法思想

按某种次序遍历二叉树，在遍历过程中用线索取代空指针即可.

(1)如果根结点的左孩子指针域为空，则将左线索标志域置1，同时给根结点加左线索。

(2)如果根结点的右孩子指针域为空，则将右线索标志域置l，同时给根结点加右线索。

(3)将根结点指针赋给存放前趋结点指针的变量，以便当访问下一个结点时，此根结点作为前趋结点。

2、二叉链表加中序线索的算法

算法与中序遍历算法类似，只是将遍历算法中访问根结点*bt的操作改为在*bt和中序前趋*pre之间建立线索。

void InorderThread(BinThrTree bt)

{　Static BinThrNode *pre=NULL；

//定义指向前趋结点的指针pre(静态变量，只初始化1次)，保存刚访问过的结点

　if(bt!= NULL) 　　　　　　　　　　　//当二叉树为空时结束递归

　　{　InorderThread(bt->lchild)；　　　//左子树线索化

　　　if(bt->lchild==NULL) bt->ltag=l；

　　　else bt->ltag=0；

　　　if(bt->rchild==NULL) bt->rtag=l ；

　　　else bt->rtag=0；

　　　if(pre)

　　　　{ if(pre->rtag==1)pre->rchild=bt；　//给前趋结点加后继线索

　　　　　if(bt->ltag==1)bt->lchild=pre； 　//给当前结点加前趋线索

　　　　}

　　　pre=bt； 　　　　　　　　　　　//将刚访问过的当前结点置为前趋结点

　　　InorderThread(bt->rchild)； 　　　　//右子树线索化

　　}

}

三、二叉线索链表上的运算

1、在中序线索二叉树上查找某结点*p的后继结点

【分析】分两种情况：

(1)若结点*p的rtag域值为1，则表明p->rchild为右线索，它直接指向结点。

(2)若结点*p的rtag域值为O，则表明p->rchild指向右孩子结点，结点*p的中序后继结点必是其右子树第一个中序遍历到的结点，因此从结点*p的右孩子开始，沿左指针链向下查找，直到找到一个没有左孩子(即ltag为1)的结点为止，该结点是结点*p的右子树中"最左下"的结点，它就是结点*p的中序后继结点。

【算法描述】

BinThrNode *InorderNext(BinThrNode *p)

{ //在中序线索二叉树上求结点*p的中序后继结点

　if(p->rtag==1)　　　　　　　　　 //rchild域为右线索

　　return p->rchild；　　　　　　 //返回中序后继结点指针

　else

　{ p=p->rchild；　　　　　　　 //从*p的右孩子开始

　　while(p->ltag==O)

　　　p=p->lchild；　　　　　　 //沿左指针链向下查找

　　return p；

　}

}

2、线索二叉树的中序遍历算法

【基本思想】首先从根结点起沿左指针链向下查找，直到找到一个左线索标志为1的结点止，该结点的左指针域必为空，它就是整个中序序列中的第一个结点。访问该结点，然后就可以依次找结点的后继，直至中序后继为空时为止。

【算法描述】

void TinorderThrTree(BinThrThrtree bt)

{ BinThrNode *p；

　if(bt!=NULL) 　　　　　　　　　　　//二叉树不空

　　{ p=bt； 　　　　　　　　　　　//使p指向根结点

　　　while(p->ltag==O)　　　　　　 //查找出中序遍历的第一个结点

　　　p=p->lchild；

　do

　　{ printf("%c"，p->data); 　　　　//输出访问结点值

　　　p=InorderNext(p)； 　　　　//调用前面的函数查找结点*p的中序后继

　　｝while(p!=NULL)； 　　　　//当p为空时算法结束

　}

}

【真题选解】