第五节 - 森林和树
发布时间:2020-09-20 10:52来源:未知
第五节 森林和树
一、树的存储结构
1、双亲表示法
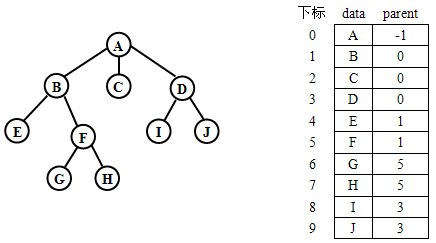
在双亲表示法中,每个存储结点由两个域组成:数据域--存储树上结点的数据元素;双亲域--存储双亲结点在结点数组中的下标值。
在这种表示法下,求指定结点的祖先很方便,但求指定结点的子孙则不方便。
2、孩子链表表示法
孩子链表表示法的基本思想是:为树上的每个结点X建立一个"孩子链表",存储X中的数据元素和指向X的所有孩子的指针。一个孩子链表是一个带头结点的单链表,单链表的头结点含两个域:数据域和指针域。其中,数据域用于存储结点X中的数据元素;指针域用于存放指向该单链表中第一个表结点(首结点)的指针。
为了检索方便,所有头结点组织成一个数组,称为表头数组。对每个结点X的孩子链表来说,其中的所有表结点也含两个域,孩子域(即数据域)和指针域。第i个表结点的孩子域存储X的第i个孩子在头结点数组中的下标值。
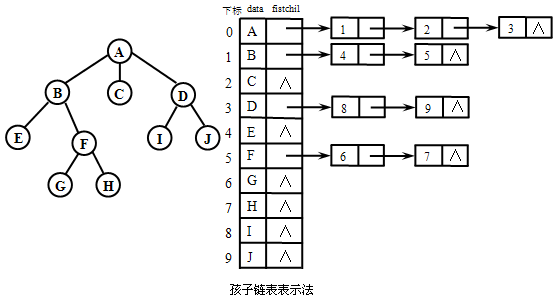
为了便于查找双亲,可在各个头结点中增加一个双亲域以存储双亲结点在头结点数组中的下标值,称其为带双亲的孩子链表表示法。

3、孩子兄弟表示法
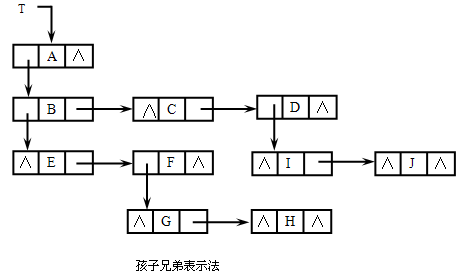
孩子兄弟表示法又称二叉链表表示法,孩子兄弟表示法中所有存储结点的形式相同,均含三个域:数据域--存储树上结点的数据元素;孩子域--存放指向本结点第一个孩子的指针;兄弟域--存放指向本结点下一个兄弟的指针。
二、树、森林与二叉树的转换
1、树、森林转换为二叉树
(1)树转换为二叉树
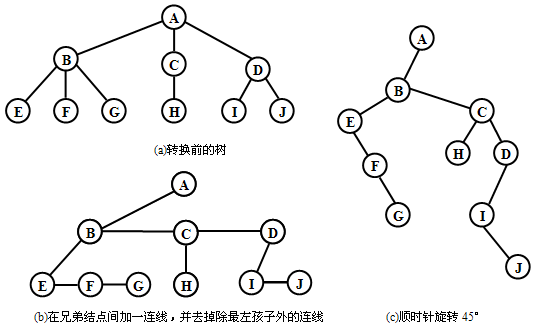
将一棵树转换为二叉树可以按以下步骤进行:
① 在所有相邻兄弟结点之间分别加一条连线。
② 对每个分支结点,除了其最左孩子外,删去该结点与其他孩子结点的连线。
③ 以根结点为轴心,顺时针旋转45°。
注意:由树转换的二叉树的根结点的右孩子始终为空,原因是树的根结点不存在兄弟结点。下图给出的例子显示了这一转换过程。
(2)森林转换为二叉树
将森林转换为二叉树的步骤可以归纳如下:
① 分别将树林中的每棵树转换为二叉树。
② 从最后那棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,直到所有二叉树全部连接,这样得到的二叉树的根结点就是树林中第一棵树的根结点。
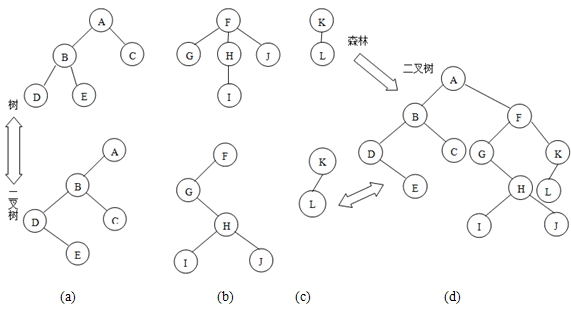
【真题选解】
(例题•选择题)森林T中有4棵树,第1、2、3、4棵树的结点个数分别是n1、n2、n3、 n4,那么当把森林T转换成一棵二叉树后,其根结点的左子树上有( )个结点。
A.n1-1
B.n1
C.nl+n2+n3
D.n2+n3+n4
(3)二叉树转换为树
将一棵二叉树转换为树可以按下列步骤进行:
① 若某结点是其双亲结点的左孩子,则将该结点的右孩子以及当且仅当连续地沿着此右孩子的右子树方向不断地搜索到的所有右孩子,都分别与该结点的双亲结点用虚线连接起来。
② 删去原二叉树中所有双亲结点与其右孩子的连线。
③ 将图形规整化,使各结点按层次排列,并且将虚线改成实线。
(4)二叉树转换为森林
将一棵二叉树转换为森林可以按下列步骤进行:
① 去掉二叉树的右子树,将去掉右子树后剩下的二叉树转换为一棵树。
② 将在第①步中被去掉的右子树再执行第①步。
③ 重复前两步,直到转换完成。
【真题选解】
(例题•简答题)已知二叉树如下:
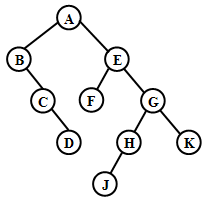
请画出该二叉树对应的森林。
三、树和森林的遍历
1、树的遍历
(1)树的前序遍历定义: ①访问根结点; ②依次前序遍历根的各子树。
(2)树的后序遍历定义: ①依次后序遍历根的各子树; ②访问根结点R。
【例】写出如图所示树的前序遍历和后序遍历的序列和该树对应二叉树的前序遍历、中序遍历和后序遍历的序列
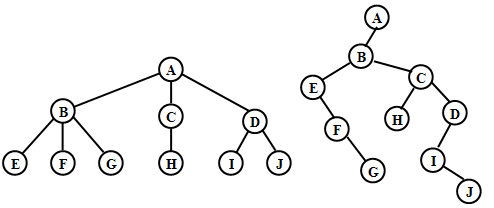
树的前序遍历序列:ABEFGCHDIJ 二叉树的前序遍历序列:ABEFGCHDIJ
树的后序遍历序列:EFGBHCIJDA 二叉树的中序遍历序列:EFGBHCIJDA
二叉树的后序遍历序列:GFEHJIDCBA
注意:
① 前序遍历一棵树恰好等价于前序遍历该树对应的二叉树;
② 后序遍历一棵树恰好等价于中序遍历该树对应的二叉树。
2、森林的遍历
(1)前序遍历森林
若森林非空,则:
①访问森林中第一棵树的根结点;
②前序遍历第一棵树中根结点的各子树所构成的森林
③前序遍历除第一棵树外其它树构成的森林。
(2)后序遍历森林
若森林非空,则:
①后序遍历森林中第一棵树的根结点的各子树所构成的森林;
②访问第一棵树的根结点;
③后序遍历除第一棵树外其它树构成的森林。
【例】写出如图所示森林的前序遍历和后序遍历的序列和该树对应二叉树的前序遍历、中序遍历和后序遍历的序列
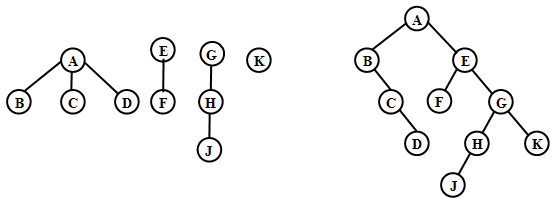
树的前序遍历序列:ABCDEFGHJK 二叉树的前序遍历序列:ABCDEFGHJK
树的后序遍历序列:BCDAFEJHGK 二叉树的中序遍历序列:BCDAFEJHGK
二叉树的后序遍历序列:DCBFJHKGEA
注意:
① 前序遍历森林等同于前序遍历该森林对应的二叉树
② 后序遍历森林等同于中序遍历该森林对应的二叉树












