第六节 - 哈夫曼树及其应用
发布时间:2020-09-20 10:54来源:未知
第六节 哈夫曼树及其应用
一、最优二叉树(哈夫曼树)
1.树的路径长度
树的路径长度是从树根到树中每一结点的路径长度之和。在结点数目相同的二叉树中,完全二叉树的路径长度最短。
2.树的带权路径长度(WPL)
结点的权:在一些应用中,赋予树中结点的一个有某种意义的实数。
结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积。
树的带权路径长度(WPL):定义为树中所有叶结点的带权路径长度之和。
3.最优二叉树或哈夫曼树
带权路径长度WPL最小的二叉树称为最优二叉树或哈夫曼树。
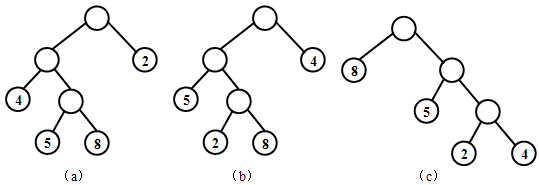
【例】给定4个叶子结点a,b,c和d,分别带权8,5,4和2。构造如下图所示的三棵二叉树(还有许多棵),它们的带权路径长度分别为:
(a):WPL=8×3+5×3+2×1+4×2=49
(b):WPL=8×3+5×2+2×3+4×1=44
(c):WPL=8×1+5×2+2×3+4×3=36
其中(c)树的WPL最小,可以验证,它就是哈夫曼树。
二、哈夫曼算法
1、构造哈夫曼树的方法:
① 将给定的权值按照从小到大排列成{W1,W2,…,Wm},并且构造出树林F={Tl,T2,…,Tm}。此时,其中的每棵树Ti (1≤i≤m)为左、右子树均为空的二叉树,二叉树的根结点的权值为Wi 。
② 把F中树根结点的权值最小的两棵二叉树T1和T2合并为一棵新的二叉树T(T的左子树为T1,右子树为T2),并令T的根结点的权值为T1和T2的根结点的权值之和,然后将T按其根结点的权值大小依次加入到树林F中。同时,从F中删去T1和T2这两棵二叉树。
③ 重复步骤②,直到构造成一棵哈夫曼树。
【真题选解】
(例题•填空题)用6个权值分别为6、13、18、30、7和16的结点构造一棵哈夫曼(Huffman)树,该树的带权路径长度为_________。
2、哈夫曼树的特点:
① 在哈夫曼树中,权值越大的叶子离根结点越近。
② 若有n0个权值,需要进行n0-1次合并,构造成为哈夫曼树。
③ 哈夫曼树没有度为1的结点。
④ 由n0个权值构成的哈夫曼树,叶结点数为n0,度为2的结点数为 n0-1,结点总数为n0+ n2= n0+ n0-1=2n0-1。
⑤ 给定一组权值,构造出的哈夫曼树的形态可能不唯一,但它们的带权路径长度都一样。
三、哈夫曼编码
1、编码的概念
(1)编码和解码
数据压缩过程称为编码。即将文件中的每个字符均转换为一个唯一的二进制位串。
数据解压过程称为解码。即将二进制位串转换为对应的字符。
(2)前缀码方案
对字符集进行编码时,要求字符集中任一字符的编码都不是其它字符的编码的前缀,这种编码称为前缀(编)码。
【真题选解】
(例题•单选题)下述编码中不是前缀码的是( )
A.(00,01,10,11)
B.(0,1,00,11)
C.(0,10,110,111)
D.(1,01,000,001)
2、哈夫曼编码
设计电文总长最短的二进制前缀编码,就是以n种字符出现的频率作为权构造一棵哈夫曼树,由哈夫曼树求得的编码就是哈夫曼编码。
【真题选解】
(例题•算法题)假设通信电文使用的字符集为{a,b,c,d,e,f,g,h},各字符在电文中出现的频度分别为:7,26,2,28,13,10,3,11,试为这8个字符设计哈夫曼编码。要求:
(1)画出你所构造的哈夫曼树(要求树中左孩子结点的权值不大于右孩子结点的权值);
(2)按左分支为0和右分支为1的规则,分别写出与每个字符对应的编码。
本章小结
本章首先介绍了一般树和二叉树的基本概念。主要介绍了四种不同的遍历二叉树算法,前三种算法的主要区别在于对一个结点本身与它的左右子树中结点的处理采用了不同的次序,而层次遍历与其他都不同。
遍历二叉树是本章的一个重点,每年必考内容。另一个重点就是使用哈夫曼算法生成哈夫曼树和构造哈夫曼编码。












