第一节 图的基本定义和术语

二、图的有关名词术语

（1）顶点的度： 所谓某个顶点V的度是指依附于该顶点的边或弧的数量，记为D（V）。 对于无向图而言，仅此而已。而对于有向图，要区分顶点的出度与入度的概念。所谓一个顶点V的出度是指以该顶点为出发点的弧的数量，记为OD（V）。所谓一个顶点V的入度是指以该顶点为终止点的弧的数量，记为ID（V）。 D（V）=OD（V）+ID（V）。

结论：① 所有顶点的度之和等于边或弧的条数2倍。

　　　② 具有n个顶点的无向图中边的数目最多为n（n-1）/2，具有n个顶点的有向图中边（弧）的数目最多为n（n-1）。

（2）路径：顶点Vx与Vy之间有路径是指存在着顶点序列Vx，Vi1，Vi2，…，Vy，并且序列中相邻两个元素构成的顶点偶对分别表示图中的一条边或弧。这里，称Vx为出发点，Vy为终止点，出发点与终止点相同的路径称为环或回路。序列中顶点不重复出现的路径称为简单路径。

对于不带权的图，两个顶点之间的路径长度是指该路径上所经过的边的数目。对于带权的图，两个顶点之间的路径长度是指该路径上所经过的边上的权值之和。

（3）子图：对于图G=（V，E）与G'=（V'，E'），若有V'V，E'E，则称G'是G的一个子图。一个图是其自身的子图。

（4）图的连通

无向图的连通：若顶点Vx与Vy之间有路径，就称Vx与Vy是连通的。若图中任意两个顶点之间都有路径，就称该无向图是连通的。

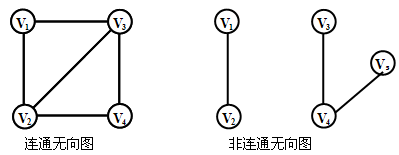
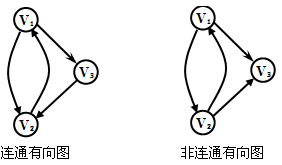
有向图的连通：若顶点Vx与Vy之间有路径，并且顶点Vy与Vx之间也有路径，就称Vx与Vy是连通的。若图中任意两个顶点之间都有连通，就称该有向图是强连通的。

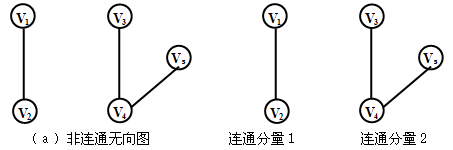
连通分量：无向图中的极大连通子图。任何一个连通图的的连通分量只有一个，是它本身。

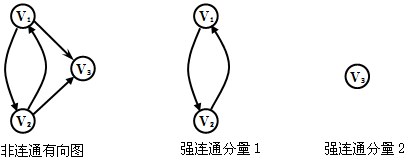
强连通分量：有向图中的极大连通子图。