第四节 - 图的生成树和最小生成树
发布时间:2020-09-20 11:00来源:未知
第四节 图的生成树和最小生成树
一、图的生成树
1、生成树的概念
对于具有n个顶点的连通图,包含了该图的全部n个顶点,仅包含它的n-1条边的一个极小连通子图被称为生成树。
一个图的生成树为一个无回路的连通图。也就是说,若在图中任意添加一条边,就会出现回路;若在图中去掉任何一条边,都会使之成为非连通图。
一个连通图的生成树不一定是唯一的。
【例】下图中图(b)和(c)是图(a)的生成树。
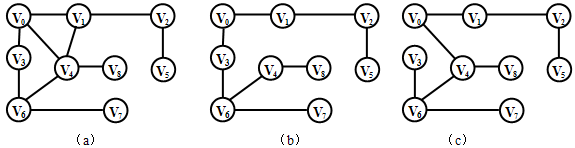
由深度优先搜索所得的生成树称为深度优先生成树,简称为DFS生成树;而由广度优先搜索所得的生成树称之为广度优先生成树,简称为BFS生成树。
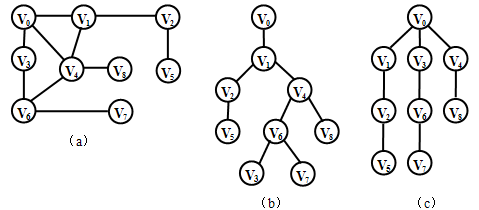
【例】下图中图(b)是图(a)从V0开始的深度优先搜索所得的生成树,图(c)是图(a)从V0开始的广度优先搜索的生成树。
从V0开始的深度优先搜索序列:V0,V1,V2,V5,V4,V6,V3,V7,V8。
从V0开始的广度优先搜索序列:V0,V1,V3,V4,V2,V6,V8,V5,V7。
二、最小生成树
1、最小生成树的概念
对于连通的带权图(网)G,其生成树也是带权的。把生成树各边的权值总和称为该树的权,把权值最小的生成树称为图的最小生成树(Mininum Spanning Tree,MST)。
【例】图(b)、(c)、(d)是图(a)的三棵生成树。
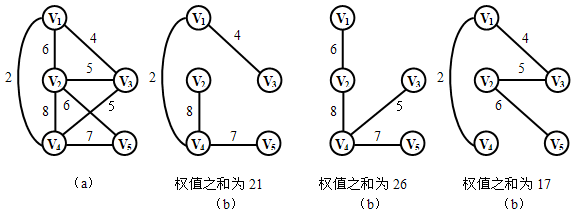
2、普里姆(Prim)算法
(1)算法思想
用自然语言描述的Prim算法:设G=(V,GE)为具有n个顶点的带权连通图,T=(U,TE)为G的一个子图,初始时,有TE=空,U={Vl},Vl∈V。Prim算法描述为:从G中选择一个顶点仅在V中,而另一个顶点在U中,并且权值最小的边加入集合TE中,同时将该边仅在V中的那个顶点加入集合U中。重复上述过程n-1次,直到U=V,此时T为G的最小生成树。
【例】试用P rim算法构造(a)图的最小生成树,要求分步给出构造过程

【分析】算法一开始取u={1},然后到V-U中找一条代价最小且依附于顶点1的边,(uo,vo)=(1,3),将vo=3加入集合U中,修改辅助数组中的值。使minedge[3].lowcost=0,以表示顶点3已并入U,由于边(3,6)上的权值是一条最小且依附于顶点集U中顶点的边,因此修改minedge[6]的值,依此类推,直到U=V,其过程如表所示。
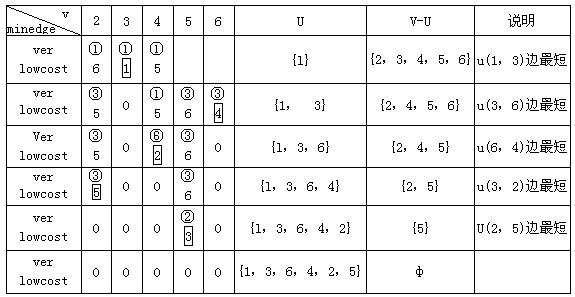
(2)算法描述
附设一个辅助数组minedge[vtxptr],记录从U到V-U具有最小代价的边。对每个顶点v∈V-U,在辅助数组中存在一个分量minedge[v],它包括两个域,其中lowcost存储该边上的权值,ver域存储该边的依附在U中的顶点。Minedge[v]=min{cost(u,v),u∈U},(cost(u,v)表示该边的权)。
【算法描述】
typedef int VRType;
typedef struct
{ertexType Ver;
VRType lowcost;
}minedge[MaxVertexNum]; //从顶点集u到V-U的代价最小的边的辅助数组
void Prim(MGraph G,VertexType u,int n)
{ //采用邻接矩阵存储结构表示图
int k,v,j;
k=vtxNum(G,u); //取顶点u在辅助数组中的下标
for(v=o;v<n;v++) //辅助数组初始化
if(v!=k)
{minedge[v].ver=u;
minedge[v].lowcost=G.arcs[k][v];
}
minedge[k].lowcost=0, //初始,U={u}
for(j=1;j<n;j++) //选择其余的n-1个顶点
{ k=min(minedge[j]);
//1≤j≤n-1,找一个满足条件的最小边(u,k),u∈u,k∈V-u
printf(minedge[k].ver, G.vexs[k]);
//输出生成树的边
minedge[k].lowcost=0; //第k个顶点并入u
for(v=0;v<n;v++)
if(G.arcs[k][v]<minedge[v].lowcost)
//重新选择最小边
{ minedge[v].ver=G.vexs[k];
mindege[v].lowcost=G.arcs[k][v];
}
}
}
普里姆算法的时间复杂度是O(n2)
【例】试用Prim算法构造下图的最小生成树,画出所有可能的情况。
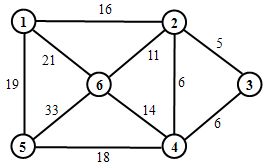
图附1-15
3、克鲁斯卡尔(Krtskal)算法
(1)算法思想
假设G=(V,E)是一个具有n个顶点的连通网,T=(U,TE)是G的最小生成树,U的初值等于V,即包含有G中的全部顶点。T的初始状态是只含有n个顶点而无边的森林T=(V,φ)。
该算法的基本思想是:将图G中的边按权值从小到大的顺序依次选取E中的边(u,v),若选取的边使生成树T不形成回路,则把它并入TE中,保留作为T的一条边;若选取的边使生成树T形成回路,则将其舍弃,如此进行下去直到TE中包含n-1条边为止,此时的T即为最小生成树。
【例】试用克鲁斯卡尔(Krtskal)算法构造(a)图的最小生成树,要求分步给出构造过程
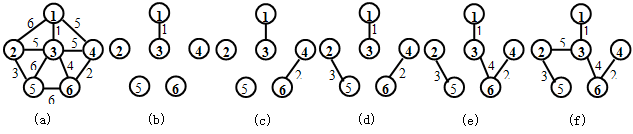
(2)算法描述
Kruskal(G)
{ //求连通网G的一棵MST
T=(v,φ); //初始化T为只含有n个顶点而无边的森林
按权值升序对边集E中的边进行排序,结果存入E[0…e-1]中
for(i=0;i<e;i++) //e为图G中边总数
{ 取第i条边(u,v);
if(u和v分别属于两棵不同的树) then
T=T ∪{(u,v)};
if(T已经是一棵树) then
return T;
}
return T;
}
克鲁斯卡尔算法的时间复杂度为O(eloge)。
注意:一个网中,若有权值相同的边,则其最小生成树不一定唯一;若所有边的权值均不相同,则其最小生成树是唯一的。












