第五节 - 最短路径
发布时间:2020-09-20 11:01来源:未知
第五节 最短路径
1、最短路径的问题
最短路径问题的提法很多,在这里仅讨论单源最短路径问题:从某个源点S∈V到G中其余各顶点的最短路径。对于求多源点的最短路径问题,可以用每个顶点作为源点调用一次单源最短路径问题算法予以解决。
【例】下图所示带权有向图,假定以vl为源点,则v1到其他各顶点的最短路径下表所示。

|
源点 |
最短路径 |
终点 |
路径长度 |
|
v1 |
v1,v3,v2 |
v2 |
5 |
|
v1 |
v1,v3 |
v3 |
3 |
|
v1 |
v1,v3,v2,v4 |
v4 |
10 |
|
v1 |
v1,v3,v5 |
v5 |
18 |
2、迪杰斯特拉(Dijkstra)算法
该算法是典型的最短路径路由算法,用于计算一个顶点到其他所有顶点的最短路径。主要特点是以起始点为中心向外层扩展,直到扩展到终点为止。
【算法思想】创建三个数组,数组S记录了当前从源点到该顶点存在最短路径的顶点集合;数组dist(简称D)记录当前状态源点到图中其余各顶点之间的最短路径长度;数组path(简称P)是最短路径的路径数组,其中path[j]表示从源点到顶点j的最短路径上顶点的前驱顶点。每一次循环都是从数组D中选择未被加入到数组S中的顶点到源点路径最短的顶点加入到数组S中,然后对数组D和数组P进行修改,直到所有顶点都加到了数组S 中为止。
【例】已知有向图如图所示,根据迪杰斯特拉算法画出求源点v1开始的单源最短路径的过程示意图,以及算法的动态执行过程。
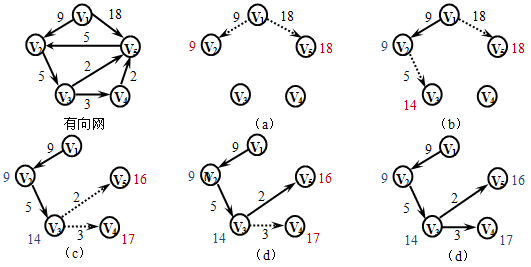
迪杰斯特拉算法的动态执行情况
| 循环 | 集合S | j | D[1] D[2] D[3] D[4] D[5] | P[1]P[2]P[3]P[4]P[5] |
| 初始化 | {1} | 1 | 0 9 ∞ 18 18 | 0 l 0 0 1 |
| 2 | {1,2} | 2 | 0 9 14 ∞ 18 | 0 1 2 0 1 |
| 3 | {l,2,3} | 3 | 0 9 14 17 16 | 0 l 2 3 3 |
| 4 | {1,2,3,5} | 5 | 0 9 14 17 16 | 0 1 2 3 3 |
| 5 | {1,2,3,5,4} | 4 | 0 9 14 17 16 | 0 1 2 3 3 |
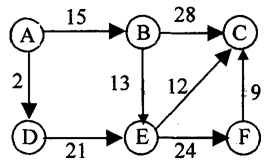
【真题选解】
(例题•填空题)已知有向图如下图所示,其中顶点A到顶点C的最短路径长度是_________。