第三节 交换排序

2、实例分析

【例】有8个记录的关键字序列为(36，28，45，13，67，36，18，56)，如下图所示为该序列起泡排序的全过程.

3、算法描述

void BubbleSort(SeqList R，int n)

{　//采用自底向上扫描数组R[1．．n]做冒泡排序

　int i，j，flag；

　for(i=1；i<n；i++) //最多做n-1趟排序

　　{ flag=0； 　　　　　　　　　　　//flag表示每一趟是否有交换，先置0

　　　for(j=n；j>=i+1；j--) 　　　　　//进行第i趟排序

　　　　if(R[j].key<R[j-1].key)

　　　　　{ R[0]=R[j-1]；　　　　　 //R[0]作为交换时的暂存单元

　　　　　　R[j-1]=R[j]；

　　　　　　R[j]=R[0]； 　　　　　　//相邻两个元素完成交换

　　　　　　　flag=1； 　　　　　　//有交换，flag置1

　　　　　}

　　　if(flag==0) return；

　　}

}

4、算法分析

（1）算法的最好时间复杂度

若待排序记录为有序(最好情况)，则一趟扫描完成，关键比较次数为n-1次且没有移动，比较的时间复杂度为O(n)。

（2）算法的最坏时间复杂度

若初始文件是反序的，需要进行n-1趟排序。每趟排序要进行n-i次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。总的比较次数为：（n-1）+（n-2）+…+1= n(n-1)/2；总的移动次数为3n(n-1)/2。在平均情况下，比较和移动记录的总次数大约为最坏情况下的一半，所以，冒泡排序算法的时间复杂度为O(n²)。

（3）算法的空间复杂度

冒泡排序的空间复杂度为O(1)，是就地排序

（4）算法稳定性

冒泡排序是稳定的。

【例】设计一个修改冒泡排序算法以实现双向冒泡排序的算法。【2009年1月考算法填空】

双向冒泡排序则是交替改变扫描方向，即一趟从下向上通过两个相邻关键字的比较，将关键字最小的记录换至最上面位置，再一趟则是从第二个记录开始向下通过两个相邻记录关键字的比较，将关键字最大的记录换至最下面的位置；然后再从倒数第二个记录开始向上两两比较至顺数第二个记录，将其中关键字较小的记录换至第二个记录位置，再从第三个记录向下至倒数第二个记录两两比较，将其中较大关键字的记录换至倒数第二个位置，依此类推，直到全部有序为止。

【算法描述】

void DbubbleSort (SeqList R，int n)

{　//自底向上、自顶向下交替进行双向扫描冒泡排序

　int i=l，j；

　RecType t；　　　　　　　　　　　　　 //t作为排序交换记录的中间变量

　int NoSwap；　　　　　　　　　　　　 //表示一趟扫描是否有交换，为假无交换

　NoSwap=1 ；　　　　　　　　　　　　 //首先假设有交换，表无序

　while (NoSwap) 　　　　　　　　　　　//当有交换时做循环

　　{　NoSwap=0；　　　　　　　　　 //置成无交换

　　　for(j=n-i+1；j>=i+l；j--) 　　　　　//自底向上扫描

　　　　if(R[j].key<R[j-1].key)　　　　　 //若反序(后面的小于前一个)，即交换

　　　　　{ t=R[j]；

　　　　　　R[j]=R[j-1]；

　　　　　　R[j-1]=t；

　　　　　　NoSwap=1；　　　　　　 //说明有交换

　　　　　｝

　　　for(j=i+1；j <=n-i；j++)　　　　 //自顶向下扫描

　　　　if(R[j].key>R[j+1].key)　　　　 //若反序(前面的大于后一个)，即交换

　　　　　{ t=R[j]；

　　　　　　R(j]=R[j+1]；

　　　　　　R[j+1]=t；

　　　　　　NoSwap=1；　　　　　 //说明有交换

　　　　　｝

　　i=i+1；

　｝

}

1、排序思想

快速排序的基本思想是：首先在当前无序区R[low…high]中任取一个记录作为排序比较的基准(不妨设为x)，用此基准将当前无序区划分为两个较小的无序区R[low…i-1]和R[i+1…high]，并使左边的无序区中所有记录的关键字均小于等于基准的关键字，右边的无序区中所有记录的关键字均大于等于基准的关键字，而基准记录x则位于最终排序的位置i上，这个过程称为一趟快速排序(或一次划分)。当R[low…i-1]和R[i+1…high]均非空时，分别对它们进行上述划分，直到所有的无序区中的记录均已排好序为止。

一趟快速排序的具体操作是：设两个指针i和j，它们的初值分别为low和high，基准记录x=R[i]，首先从j所指位置起向前搜索找到第一个关键字小于基准x.key的记录存入当前i所指向的位置上，i自增l，然后再从i所指位置起向后搜索，找到第一个关键字大于x.key的记录存入当前j所指向的位置上，j自减1；重复这两步，直至i等于j为止。

2、实例分析

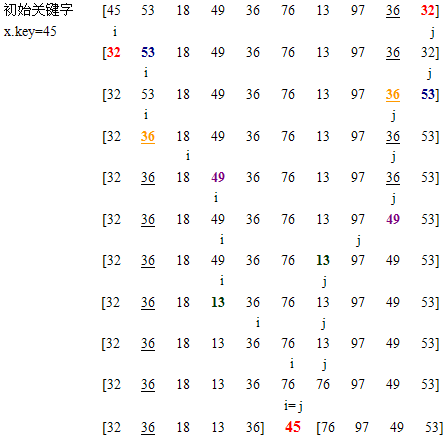
依次可得各趟排序结果如下：

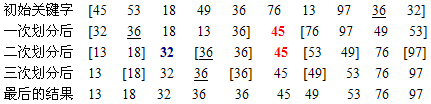
3、算法描述

int Partition(SeqList R，int i，int j)

{　//对R[i]…R[j]区间内的记录进行一次划分排序

　RecType x=R[i]； 　　　　　　　　　　　　　//用区间的第一个记录为基准

　while(i<j)

　　{ while(i<j&&R[j].key>=x.key)

　　　　　j--； 　　　　　　　　　　　　　　//从j所指位置起向前(左)搜索

　　　if(i<j)

　　　　{ R[i]=R[j]；i++；　　　　　　　　　 //后面大的数往前移动

　　　　}

　　　while(i<j&&R[i].key<=x.key)

　　　　　　i++； 　　　　　　　　　　　　//从i所指位置起向后(右)搜索

　　　if(i<j)

　　　　{ R[j]=R[i]；j--；　　　　　　　　　 //前面小的数往前移动

　　　　｝

　　｝

R[i]=x；　　　　　　　　　　　　　　　　　 //基准记录x位于最终排序的位置i上

return i；

｝

void QuickSort(SeqList R，int low，int high)

｛　//对顺序表R中的子区间进行快速排序

　int p；

　if(low<high) //长度大于1

　{　p=Partition(R，low，high)；　　　　　　　 //做一次划分排序

　　QuickSort(R，low，p-1)； 　　　　　　　　//对左区间递归排序

　　QuickSort(R，p+l，high)；　　　　　　　　 //对右区间递归排序

　｝

｝

4、算法分析

（1）算法时间复杂度

快速排序的时间复杂度为O（nlog₂n）。快速排序方法被认为是排序时间效率非常高的一种方法，但是，当参加排序的原始序列已经是一个按值有序或基本有序的序列时，快速排序方法的时间效率将降到最低，这种情况下其时间复杂度为O（n²）

（2）算法空间复杂度

快速排序的空间复杂度为O（log₂n）。

（3）算法的稳定性

快速排序方法是一种不稳定的排序方法。